Honors Calculus I+II Combined Academic Credit Online Course For Data Science
A very popular academic goal is pursuit of advanced degrees in Data Science and related fields, which necessitates a strong background in freshman and sophomore level calculus.
Honors Calculus I+II for Data Science [DMAT 255 - Honors Calculus I+I For Data Science - 5 credits] is an accelerated, combined course for freshman calculus, specifically assembled for Data Science students. Set at the Honors level, DMAT 255 is equivalent to AP Calculus BC which bridges Calculus I and Calculus II topics in a single course/year, and upon completion, is equivalent to completion of Calculus II (DMAT 263/264).
| Course Title: | Honors Calculus I+II for Data Science |
| Catalog Number: | DMAT 255 |
| Credits: | 5 Semester Credit Hours |
| Syllabus PDF: | PDF Syllabus for Honors Calculus I+II for Data Science |
| Delivery: | Fully Online, Asynchronous, Self-Paced |
| Click Here to Enroll in DMAT 255 - Honors Calculus I+II for Data Science | |
DMAT 255 - Honors Calculus I+I For Data Science - 5 credits provides the data science-bound student with a single course re-entrance in the calculus curriculum to come up to speed with freshman calculus more quickly than having to take two separate courses in succession.
Honors Calculus I+I For Data Science engages the traditional freshman calculus topic set, beginning with derivatives, then moving on into integration theory, then onto polynomial approximations (Taylor's Theorem), preparing the DMAT 255 student for the various Sophomore level courses, such as Linear Algebra, Multivariable Calculus, Differential Equations, and the very important Probability Theory.
Many Data Science-bound students ask "How many math courses should I take to prepare for a Data Science degree?"
Being a data scientist means you will simultaneously be a mathematician, a statistician (these are not! the same!), and a computer programmer. As a multi-disciplinarian, you need to be a "jack of all trades" as the saying goes.
DMAT 255 - Honors Calculus I+I For Data Science - is offered at the Honors level, because of the calibre of data science-bound students.
Nationally, "Honors" courses usually are centered on a mathematically rigorous development of the concepts of calculus, bringing many advanced topics from upper division courses such as Advanced Calculus and Real Analysis into the freshman honors calculus courses. While this may be a worthwhile approach for students who seek to become mathematics majors, it creates, for many students, an inflated level of course difficulty of questionable benefit to related fields of study.
Our approach to Honors courses is built upon a distinctly different educational philosophy:
- Freshman & Sophomore Calculus is NOT the correct math level to increase rigor
We believe that mathematical rigor is learned after exposure to the calculus, in the upper division, after some time and maturing of mathematical thought is allowed to organically develop. No student ever understood the concept of a derivative because the natural numbers were first axiomatically developed. - Honors means DEEPER, not just HARDER
In mathematics, the potential for making any course harder is a rather simple proposition. Work SMARTER, not HARDER mandates that an honors course should not be more difficult just to say it is. A true honors student wants to go deeper into the topics, not flirt with academic demoralization via some mathematical bootcamp experience. - Technical Writing Curriculum
While axiomatic development has its place in upper division math, core improvement of technical writing skills will benefit all students in all disciplines with immediate effect. If calculus is supposed to be mathematical preparation for science, technology, and engineering related fields, then development of technical writing skills should be as important as computational prowess. - Course Term Paper
Each Honors course student will write a 10-20 page term paper on a topic chosen in collaboration with the course instructor, empowering the student to simultaneously improve technical writing skills and deepen knowledge in the student's chosen academic field via a uniquely creative exercise that will transcend the traditional course boundaries.
In summary, our Honors courses go deeper and broader in the curriculum, offer a notch more challenging course work set, and featuring a technical writing curriculum that truly prepares the student for further academics in the sciences.
Completion of DMAT 255 - Honors Calculus I+II for Data Science earns 5 academic credit semester hours with an official academic transcript from Roger Williams University, in Providence, Rhode Island, USA, which is regionally accredited by the New England Commission of Higher Education (NECHE), facilitating transfer of credits nationwide to other colleges and universities.
DMAT 255 - Honors Calculus I+II for Data Science is offered in the Fall, Winter, Spring, and Summer semesters with "revolving enrollment", which means you may enroll at any time, and start your course whenever you wish, independent of the traditional academic calendar.
DMAT 254 Honors Calculus I+II For Data Science differs from the mainstream DMAT 253 STEM Calculus I and DMAT 254 Honors STEM Calculus I courses in the following ways:
| DMAT 253 STEM Calculus I |
DMAT 254 Honors STEM Calculus I |
DMAT 255 Honors Calculus I+II for Data Science |
|
| Precalculus Refresher |
Yes | No | No |
| Limits | Graphical, Numerical, Basic Algebraic | + Cantor Sets, Limits by Functional Comparison, Graphical ε/δ, Numerical Analysis Issues, L'Hopital | Abbreviated Limits, Numerical Analysis Issues |
| Derivatives | Graphical, Numerical, Algebraic Rules | + Non-Differentiable Functions | + Machine Derivative Issues |
| Applications of Derivatives |
Basic Optimizations | + Applications To Physics, Economics, Data Analysis | + Applications To Data Science |
| Differential Equations |
Linear, Logistical | + Polynomial Approximations, Systems, Preditor-Prey | + Applications to Data Science |
| Integration | Graphical, Numerical, Algebraic Antiderivatives, Fundamental Theorem of Calculus | + Numerical Integration Techniques, Monte-Carlo Method, Integration in Finite Terms | + Data Science Integration Issues |
| Data Analysis | Functions Defined by Data | + Rational Polynomial and Trigonometric Approximation | + Data Interpolation |
| Integration Techniques |
u-substitution Integration by Parts |
+Integration via Differentiation, Iteration, Complex Exponentials | +Data Interpolation, Iteration, Computable Limits |
| Fundamental Theorem |
Functions Defined By Integrals | +Generalization of Trigonometric Functions to Elliptic Functions | +Special Functions |
| Geometric Measurements |
Double Integrals over Rectangularish Regions, Surfaces of Revolution, Green's Theorem, Fubini's Theorem (Interchange Order of Integration) | + Higher Questions on Parameterization of the Boundary, Parameterization of Algebraic Curves, Interpolation of Boundary Data | + Connection to Data Measurements |
| Numerical Integration |
Euler | + Midpoint, Runga-Kutta, Higher Estimates, Monte-Carlo Method | + Machine Integration Techniques |
| Sequences Series |
Ratio, Integral Convergence Tests | + Root, Raabe's, p-Test, Machine Convergence Limitations, Famous Infinite Sums from Number Theory, Ramanujan's Summation | + Abbreviated |
| Polynomial Approximations |
Taylor's Theorem | + Applications to Differential Equations, Rational Polynomial Approximations, Computing π | + Data Splining |
| Integration Theory |
Quadrature of Rational Polynomials, Exponential, and Trigonometric Functions | + Integration in Finite Terms, Near Finite-Term Integrals, Liouville's Theorem, Machine Integration Engines | + Limitation of Machine Integration |
| Technical Writing | Basic Exposition in Homework Problems |
+ Technical Writing Curriculum, Term Paper | + Term Paper Includes Programming Project on Topic from Data Science |
HONORS Course Information Video
Honors Courses via Distance Calculus
Video Time: 11 minutes
Introduction to Calculus I Course
Video Time: 22 minutes
Introduction to Calculus II Course
Video Time: 22 minutes
Honors Calculus I+II for Data Science - DMAT 255 - Introduction
Freshman Calculus is the gateway to collegiate mathematics. As such, Freshman Calculus is often a prerequisite course for many majors, both science and non-science.Calculus I introduces the fundamental concept of the derivative, geometrically demonstrated in this animation showing a limit of secant lines approaching a tangent line at a point on a curve y=f(x):
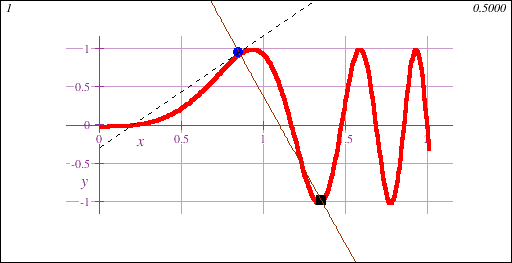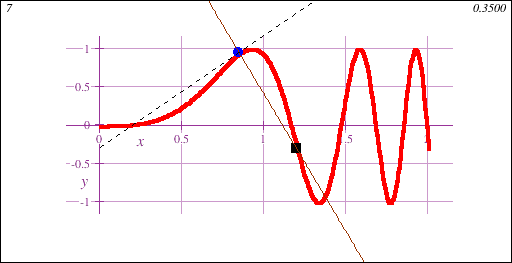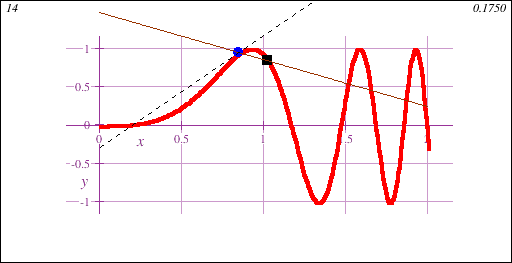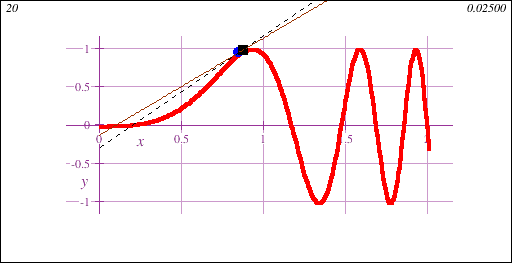
Freshman Calculus also introduces the fundamental concept of the integral, geometrically demonstrated in this animation showing the accumulation of signed area under a curve y=f(x) of increasing accuracy:
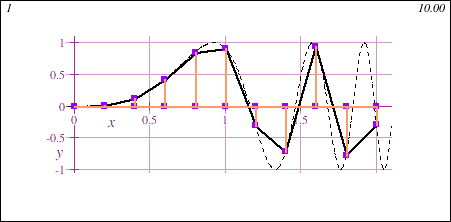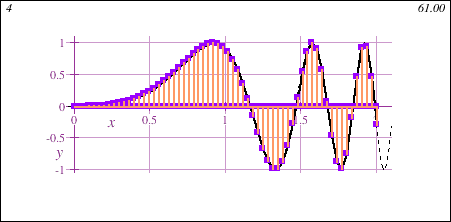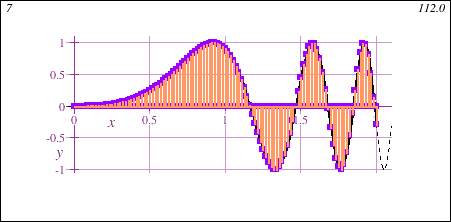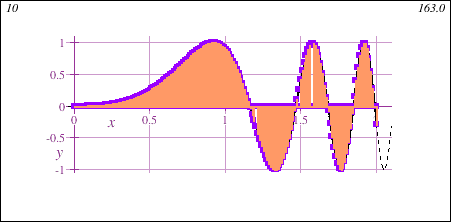
Main Themes of Honors Calculus I+II for Data Science - DMAT 255
- Differential Calculus
STEM Calculus I begins with investigating the phenomena of growth of the various types of functions, culminating with the derivative as a measurement of growth. Limits of functions and their usage in formulating the algebraic rules for computing derivatives - Newton's "calculus" - are examined both in classical algebraic terms, and numerically and graphically with modern computer algebra and graphing tools. Applications of the derivative to "max/min" problems, differential equations, related rates, implicit differentiation, sum/product/chain rules, rates of change, and parametric equations are then studied. - Integration Theory
When you (or a computer) can algebraically integrate a function, how is that accomplished? Essentially, the Rules of Differentiation are "inverted" to the integral, providing the main strategies for attacking the algebraic integral - when possible. - Techniques of Integration
One of the goals of Calculus II is to become an expert in algebraic integration: finding antiderivatives. Computer algebra tools can find antiderivatives automagically, so an exploration of the techniques of antiderivatives must contain an meaningful mixture of integration concepts, manual skills, and usage of computer algebra software. Traditional Calculus II courses explore these techniques purely from the paper/pencil standpoint, which has merits and drawbacks in this modern age. We strive for a balance between classical and modern computational mathematics in a unique way. For example, a more advanced integration technique known as Integration via Differentiation is presented, which is absent from all traditional textbooks, since it is computationally difficult with only manual tools - it is the leverage of computer algebra tools that makes this technique come alive. - Double Integrals and Gauss-Green Theorem
Calculus II starts the dimensional generalization of integration theory, into double (or 2D) integrals, which can be used to measure volume and other applications. Double integrals initially come in two varieties: over 2D regions that are essentially rectangular, and over 2D regions that are not rectangular, but whose boundary curve can be formulated. In the latter case, the Gauss-Green Theorem is utilized; it is common for this theorem to be explored only in Multivariable Calculus, but we do this theorem early as an introduction to the higher dimensional Fundamental Theorem of Calculus. - When Algebraic Integration Just Can't Be Done
The vast majority of functions cannot be algebraically integrated - there just is no algebraic antiderivative for such functions. The development of "Plan B" for attacking these types of algebraic integrals comes in the form of expanding the way we describe functions, not just with the elementary class of functions including such friends as sin(x), ex, x1/2, etc. but with a more generalized description based upon infinite polynomials. This raises all kinds of questions that have to be studied, but once accomplished, we are able to conquer these algebraic integrals. - Introduction to Vector Calculus
To meet transferability requirements, Calculus II has a few introductory lessons on 3D geometry: lines, planes, vectors, dot products, cross products.
Roger Williams University Course Catalog Listing: DMAT 255 - Honors Calculus I+II for Data Science
Course: DMAT 255
Course Title: Honors Calculus I+II for Data Science
Transcript Course Title (30 Characters Max:): Honors Calc BC for Data Sci
Course Description: An honors-level single course introduction to differential and integral calculus for data science students, with emphasis on a modern, empirical exposition of the classical subject, condensing the essential topics from first year calculus. Topics include a study of the algebraic, numerical, and graphical aspects of polynomial, exponential, logarithmic, and trigonometric functions, limits, function growth, derivative analysis and optimization, introduction to differential equations, methods and applications of integration, the Fundamental Theorem of Calculus, calculus of data sets, numerical issues of derivative and integral computations, Monte-Carlo method, Taylor's Theorem and spline approximations, and methods of integration. Honors courses will include greater breadth and depth of topics, and develop technical writing skills, culminating in a combination programming project and mathematical term paper on an approved topic. [5 Semester Credits]
Prerequisite: Successful completion with B grade or higher in Precalculus with Trigonometry or equivalent, or consent of instructor; experience with a computer programming language.
E-Textbook: Calculus&Mathematica by Davis/Porta/Uhl
Software: Mathematica
PDF Course Syllabus: Detailed Course Syllabus in PDF for DMAT 255 - Honors Calculus I+II for Data Science
DMAT 255 - Honors Calculus I+II for Data Science - Learning Outcomes
- 1. To understand and compute algebraic, numerical, and graphical limits at finite and infinite values;
- 2. To understand and compute the fundamental concept of the derivative;
- 3. To understand and compute various measurements of growth of a function
- 4. To algebraically compute derivatives of common functions using summation, product, quotient, and chain rules for derivatives;
- 5. To understand and compute optimization of functions using derivatives, finding critical values;
- 6. To understand and compute the second derivative;
- 7. To understand and compute first order differential equations;
- 8. To understand and compute parametric equations, including projectile motion;
- 9. To understand and calculate numerically and graphically the core concepts of the integral for applications to signed area measurements;
- 10. To compute numerically, algebraically, and graphically integrals of a variety of functions;
- 11. To algebraically compute integrals of basic polynomial, exponential, and trigonometric functions, with an introduction to the algebraic substitution technique;
- 12. To use of tools of differential and integral calculus in various applications
- 13. To understand and compute the Fundamental Theorem of Calculus
- 14. To understand and compute an integral functions, including inverse trigonometric and logarithmic integrals that do not algebraically resolve;
- 15. To utilize computer algebra and graphing software to amplify traditional manual computation techniques.
- 16. To understand spline interpolation with polynomial functions; points of contact
- 17. To understand Taylor's Theorem, error analysis
- 18. To understand convergences and divergence concepts of sequences, series, polynomial approximations
- 19. To understand and compute double integrals
- 20. To understand and compute 3D vector analysis, dot product, planes, and cross products
- 21. To understand and compute partial derivatives and tangent planes to a surface
- Honors Additional Topics:
- 22.* To investigate data interpolation and algebraic modeling of data sets using polynomial and trigonometric functions
- 23.* To investigate numerical limits error analysis, the need for Lagrange, Newton, L'Hopital, Extrapolation, more advanced polynomial and rational polynomial approximation methods.
- 24.* To understand the concept of algebraic integration in Finite Terms
- 25.* To understand and compute integrals using complex integration techniques
- 26.* To understand and compute numerical integration techniques of Newton, Midpoint, and Runge-Kutta, and higher RK approximations.
- 27.* To understand and explore higher integral functions, such as those defined by elliptical and hyperbolic integrals
- 28.* To explore and analyze Preditor-Prey systems of differential equations
- 29.* To develop mathematical technical writing skills, culminating in a term paper on an approved topic
- 30.* To utilize programming-based computer algebra software to make investigations for a programming term project in application to data science
- * = Additional topics for Honors course
DMAT 255 - Honors Calculus I+II for Data Science - Syllabus of Topics
1. Getting Started 1.1 Email and Chat 1.2 Learning About the Course 1.3 Required Hardware 1.4 Software Fundamentals 2. Growth: Preparing for the Derivative 2.1 Growth of Linear Functions 2.2 Growth of Power Functions 2.3 Growth of Exponential Functions 2.4 Dominance of Growth of Functions 2.5 Percentage Growth of Functions 2.6 Global Scale: Infinite Limits 2.7 Data Functions and Interpolation 2.8 Approximation of Functions by Linear Functions 3. Continuity 3.1 Limits 3.2 Continuous Functions 3.3 Jump Discontinuities 3.4 Piecewise Functions and Continuity 3.5 Limit Rules 4. Exponential Functions and Natural Logarithms 4.1 e = Euler's Number 4.2 Natural Logarithm 4.3 Growth Analysis 4.4 Applications: Carbon Dating 4.5 Percentage Growth and Steady Growth of Exponential Functions 4.6 Data Functions and Logarithmic Analysis 4.7 Inverse Functions 4.8 Applications: Compound Growth Rates 4.9 Applications: World Population 5. The Derivative of Polynomial, Exponential, Logarithmic, and Fractional Powers 5.1 Instantaneous Growth Rates 5.2 Definition of the Derivative 5.3 Computing the Derivative Graphically 5.4 Computing the Derivative Algebraically 5.5 Computing the Derivative Numerically 5.6 Average Growth Rate vs. Instantaneous Growth Rate 5.7 Applications of the Derivative: Spread of Disease 5.8 Finding Maxima and Minima of Functions 5.9 Relating a Function and Its Derivative 6. Computing Derivatives 6.1 Sum, Difference, Product, Quotient Rule 6.2 Chain Rule 6.3 Instantaneous Percentage Growth 6.4 Growth Dominance 7. Using Derivatives 7.1 Finding Maxima and Minima 7.2 Finding Good Representative Plots 7.3 Applications: Maximizing Volume 7.4 The Second Derivative 7.5 Applications: The Space Shuttle Challenger 8. Integration 8.1 Measuring Area Under a Curve 8.2 Definition of the Integral 8.3 Properties of Integrals, Symmetry 8.4 Integrals of Data Functions 8.5 Numerical Methods: Rectangles, Trapezoids 8.6 Undefined Integrals 8.7 Numerical Calculation of Integrals 8.8* Monte-Carlo Method of Integration 9. Fundamental Theorem of Calculus 9.1 Derivative of an Integral 9.2 Integral of a Derivative 9.3 Fundamental Formula 9.4 Distance, Velocity, and Acceleration 9.5 Improper Integrals 9.6 More Properties of Integrals 9.7 Applications: Measure Accumulation Totals 9.8 Indefinite Integrals and Antiderivatives 9.9 u-Substitution 9.10 Inverse Circular and Hyperbolic Trigonometric Functions 10.* Limits Revisited 10.1* Limitations of Numerics with Limits 10.2* Lagrange, Newton, Extrapolation Numerical Methods 10.3* L'Hopital's Rule for Limits 11.* Preditor-Prey Systems 11.1* Parametric Solutions of Differential Equations 11.2* Preditor-Prey Models 11.3* Applications 12.* Data Interpolation 12.1* Linear and Quadratic Approximations 12.2* Polynomial Approximations and Interpolation 12.3* Trigonometric Function Interpolation 13.* Algebraic Integration Theory 13.1* Machine Integration Engines 13.2* Integration in Finite Terms 13.3* Integratability and Limitations 13.4* Defining advanced special functions using integrals or series 14. Taylor's Expansion of a Function 14.1 Splines and Smooth Splines 14.2 Points of Contact 14.3 Application: Landing an Airplane 14.4 Taylor Expansion 14.5 Recognizing Familiar Expansions 14.6 Using Expansions for Approximations 14.7 Derivatives and Integrals of Expansions 14.8 Expansions At Other Points 14.9 Newton's Method 14.10 Convergence Intervals and Barriers 14.11 Calculating Limits: L'Hopital's Rule 14.12* Expansions and Solving Differential Equations 14.13* Complex Exponentials 14.14* Euler, Midpoint, Runge-Kutta Integral Estimates 15.* Differential Equations 15.1* Types of Differential Equations 15.2* Linkage to Algebraic and Numerical Integration Theory 15.3* Power Series Solutions to Differential Equations 15.4* Elliptical and Hyperbolic Integration Functions 15.5* Exploring Special Named Functions 16. Polar Coordinates 16.1 Basic Graphing 16.2 Recognizable Curves 16.3 Differentiation and Integration in Polar Coordinates 17. Vector Analysis 17.1 Vector Arithmetic 17.2 Dot Product, Cross Product 17.3 Planes 17.4 Partial Derivatives 17.5 Tangent Planes 18.* Mathematical Writing 18.1* Cogent writing 18.2* Mathematical Presentation 18.3* Term Paper Topic and Research
Distance Calculus - Student Reviews





Date Posted: Jan 19, 2020
Review by: Dan P.
Courses Completed: Calculus I, Calculus II
Review: I found the courses to be informative, enjoyable, and most importantly, effective in helping me learn the concepts of calculus. My math skills were always very weak, and I had a great deal of difficulty passing my undergrad math courses. The pace of a traditional classroom setting was just too quick for the concepts to really sink in. With Distance Calculus, I had courses that were taught with the full rigor of an on-campus class, but where I could take my time and really learn the material...all while having access to top-tier instructional help for real math professors and assistants. DC gave me the tools and the confidence I needed, so after successfully passing my DC courses, I moved on and completed a master's degree in CS.





Date Posted: Feb 23, 2020
Review by: Carl Conners
Courses Completed: Multivariable Calculus, Differential Equations, Linear Algebra
Review: After a really rough first year of calculus, I completed all of the second year calculus courses with Distance Calculus. It was like night and day the difference. My first year was so boring and monotonous. Multivariable Calculus, Differential Equations, and Linear Algebra through Distance Calculus were just so much different - so not boring at all. I thoroughly enjoyed these courses. So engaging.
Transferred Credits to: Michigan State University





Date Posted: Apr 29, 2020
Review by: Harlan E.
Courses Completed: Calculus I, Calculus II
Review: I did not do well in AP Calculus during my senior year in high school. Instead of trying to cram for the AP exam, I decided to jump ship and go to Distance Calculus to complete Calculus I. This was awesome! I finished Calculus I in about 6 weeks, and then I kept going into Calculus II. I started as a freshman at UCLA with both Calculus I and II done!
Transferred Credits to: University of California, Los Angeles
 Freshman Math Courses
Freshman Math Courses
- Applied Calculus for Business [3 credits] [3CR]
- Applied Calculus for Life Science [3 credits] [3CR]
- Calculus I[4 credits] [4CR]
- Calculus II[4 credits] [4CR]
 Sophomore Math Courses
Sophomore Math Courses
- Multivariable Calculus III [4 credits] [4CR]
- Differential Equations [3 credits] [3CR]
- Linear Algebra [4 credits] [4CR]
- Probability Theory [3 credits] [3CR]
 Honors Math Courses
Honors Math Courses
- Honors Calculus I [5 credits] [5CR]
- Honors Calculus II [5 credits] [5CR]
- Honors Calculus I+II for Data Science [5 credits] [5CR]
- Honors Multivariable Calculus [5 credits] [5CR]
- Honors Differential Equations [4 credits] [4CR]
- Honors Linear Algebra [5 credits] [5CR]
- Honors Linear Algebra for Data Science [5 credits] [5CR]
 Lower Division Math Courses
Lower Division Math Courses
- Precalculus with Trigonometry [4 credits] [4CR]
- Introductory Statistics [4 credits] [4CR]
- Finite Mathematics [3 credits] [3CR]
- Discrete Mathematics [4 credits] [4CR]
 Upper Division Math Courses
Upper Division Math Courses
- Computational Abstract Algebra [4 credits] [4CR]
- Computational Differential Geometry [4 credits] [4CR]

